引入

给定一个 r 行的数字三角形（r<=1000），需要找到一条从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到当前点左下方的点或右下方的点。

    7
   3 8
  8 1 0
 2 7 4 4
4 5 2 6 5

在上面这个例子中，最优路径是7-3-8-7-5 。

最简单粗暴的思路是尝试所有的路径。因为路径条数是 O(2^r) 级别的，这样的做法无法接受。

对于每一个点，它的下一步决策只有两种：往左下角或者往右下角（如果存在）。因此只需要记录当前点的最大权值，用这个最大权值执行下一步决策，来更新后续点的最大权值。
通俗来说，只需要考虑当前点左下角和右下角哪个值最大，就往哪个点走。

这时候还存在一个问题：子问题间重叠的部分会有很多，同一个子问题可能会被重复访问多次，效率还是不高。解决这个问题的方法是把每个子问题的解存储下来，通过记忆化的方式限制访问顺序，确保每个子问题只被访问一次。

上面就是动态规划的一些基本思路。下面将会更系统地介绍动态规划的思想。

Main

进入正题。
先看看学术解释：

动态规划（Dynamic Programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

动态规划的基本思想

动态规划的基本思想就是将待求解的问题分解成若干个子问题，先求解子问题，再从这些子问题的解得到原问题的解。与分治法不同的是，分治法的子问题通常是相互独立的，而动态规划的子问题往往不是相互独立的¹。

动态规划的核心元素：
动态规划的实现依赖于三个主要的概念：最优子结构、边界和状态转移方程。找到这三个条件，一般就能solve Problem了。

• 最优子结构：一个问题的最优解包含其子问题的最优解。这意味着可以通过组合子问题的最优解来构造整个问题的最优解。
• 边界：问题的边界是最简单的子问题，它们可以直接解决。在动态规划中，边界通常是递归算法的基本情况。
• ※状态转移方程：这是一个公式，它描述了问题的当前状态如何从前一个或多个较小的状态转换而来。状态转移方程是动态规划的核心，它定义了如何通过较小的子问题的解来找到较大的子问题的解。

动态规划的过程

动态规划的过程通常包括以下几个步骤：

1. 定义状态：首先需要定义问题的状态，即问题的各个阶段。
2. 状态转移：然后确定状态之间的转移方式，即如何从一个或多个状态转移到另一个状态。
3. 初始化边界：确定动态规划的边界，即最简单的子问题的解。
4. 计算顺序：确定计算状态的顺序，通常是按照自底向上的方式，先计算子问题，再逐步求解更大的问题。
5. 构造最优解：最后根据计算出的状态和状态转移方程，构造问题的最优解。

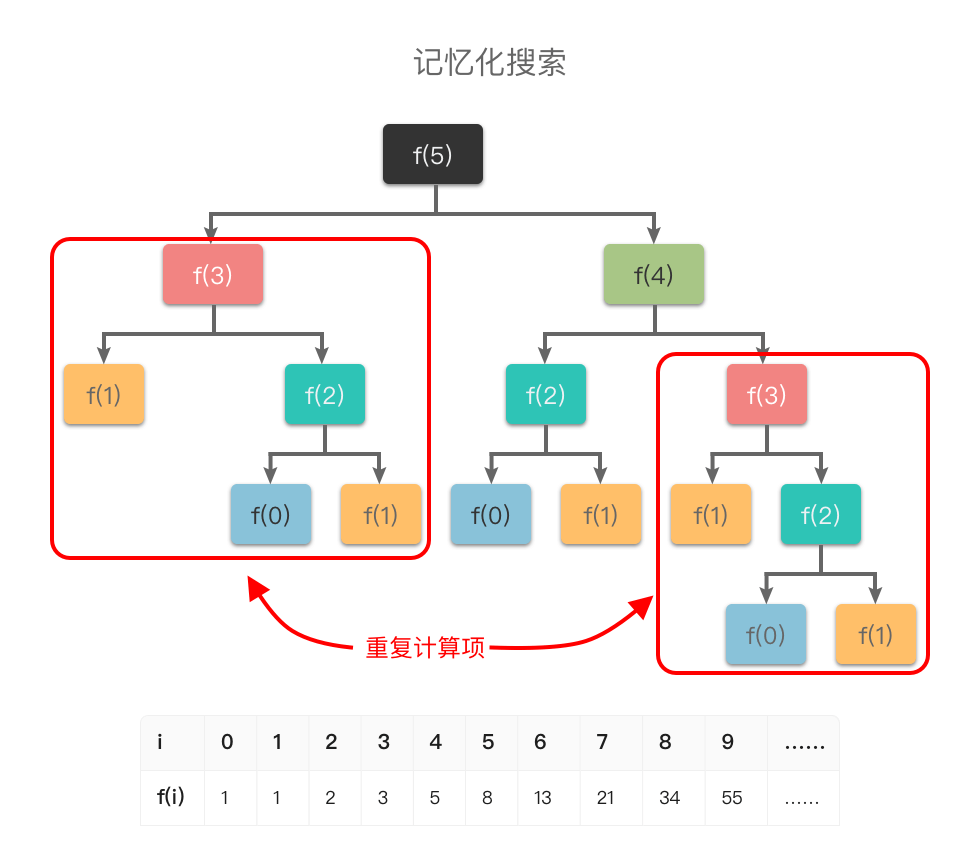
示例：斐波那契数列

斐波那契数列是动态规划中常见的一个例子。斐波那契数列的递归实现非常简单，但效率低下，因为它会重复计算许多子问题。使用动态规划，我们可以存储已经计算过的子问题的解，避免重复计算，从而大大提高效率。

def fibonacci(n):
    # 初始化存储子问题解的数组
    f = [0] * (n + 1)
    f[0], f[1] = 0, 1
    for i in range(2, n + 1):
    f[i] = f[i - 1] + f[i - 2]
    return f[n]

在这个例子中，我们定义了斐波那契数列的状态为 f[i]，即第 i 个斐波那契数。状态转移方程为 f[i] = f[i – 1] + f[i – 2]，边界条件为 f[0] = 0 和 f[1] = 1。我们从 i = 2 开始计算，直到 i = n，最终得到第 n 个斐波那契数。

动态规划的判断

能用动态规划解决的问题，需要满足三个条件：最优子结构，无后效性和子问题重叠。

最优子结构

具有最优子结构也可能是适合用贪心的方法求解。

注意要确保我们考察了最优解中用到的所有子问题。

1. 证明问题最优解的第一个组成部分是做出一个选择；
2. 对于一个给定问题，在其可能的第一步选择中，假定你已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的，只是假定已经知道了这种选择；
3. 给定可获得的最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间；
4. 证明作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。方法是反证法，考虑加入某个子问题的解不是其自身的最优解，那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解，从而得到原问题的一个更优的解，从而与原问题最优解的假设矛盾。

要保持子问题空间尽量简单，只在必要时扩展。

最优子结构的不同体现在两个方面：

1. 原问题的最优解中涉及多少个子问题；
2. 确定最优解使用哪些子问题时，需要考察多种选择。

子问题图中每个定点对应一个子问题，而需要考察的选择对应关联至子问题顶点的边。

无后效性

已经求解的子问题，不会再受到后续决策的影响。

子问题重叠

如果有大量的重叠子问题，我们可以用空间将这些子问题的解存储下来，避免重复求解相同的子问题，从而提升效率。

基本思路

对于一个能用动态规划解决的问题，一般采用如下思路解决：

1. 将原问题划分为若干 阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为 状态）；
2. 寻找每一个状态的可能 决策，或者说是各状态间的相互转移方式（用数学的语言描述就是 状态转移方程）。
3. 按顺序求解每一个阶段的问题。

如果用图论的思想理解，我们建立一个有向无环图，每个状态对应图上一个节点，决策对应节点间的连边。这样问题就转变为了一个在 DAG 上寻找最长（短）路的问题（参见：DAG 上的 DP）。

参考资料与注释

1. 动态规划基础 – OI Wiki