例1 数字三角形

下图给出了一个数字三角形，请编写一个程序，计算从顶至底的某处的一条路径，使该路径所经过的数字的总和最大。

1. 每一步可沿左斜线向下或右斜线向下
2. 三角形数字为自然数

         7
       3  8
     8   1  0
  2   7   4   4
4   5   2   6   5

输入格式

第 1 行是输入整数（如果该整数是00 ,就表示结束，不需要再处理），表示三角形行数 n 。

然后是n行数。

输出格式

输出最大值。

样例输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出

30

数据范围与提示

对于 30% 的数据 n≤10
对于 60% 的数据 n≤200
对于 100% 的数据，设三角形中最大数为 maxa ， 则 n≤2000 , maxa≤10000。
时间限制：1000ms
空间限制：65536kb

分析

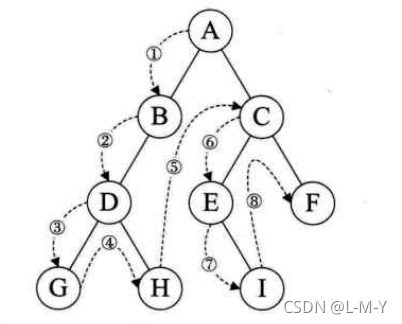
每次可以往左，或往右，具体该往哪边走，是没有规律可言的，显然可以用dfs搜索，所谓搜索就是尝试完所有的可能性。

#include <bits/stdc++.h>
using namespace std;
int a[2005][2005],ans,n;

void dfs(int x,int y,int sum) // 从（1，1）到（x，y）当前路径的总和是sum
{
    if(x==n)
    {
        ans=max(ans,sum);
        return;
    }
    dfs(x+1,y,sum+a[x+1][y]);
    dfs(x+1,y+1,sum+a[x+1][y+1]);
}
int main()
{
    cin >> n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin >> a[i][j];
    dfs(1,1,a[1][1]);
    cout << ans;

}

20分，超时是必然的，原因是很多状态被重复计算，导致了时间的浪费。

考虑剪枝，记录下从（1，1）到（x，y）路径和的最大值f[x][y]，如果某条路径到（x，y）的路径和的值小于f[x][y]，没必要再继续走下去。

#include <bits/stdc++.h>
using namespace std;
int a[2005][2005],ans,n,f[2005][2005];

void dfs(int x,int y,int sum)
{
	if(sum<=f[x][y]) return;
	f[x][y]=sum;
	if(x==n)
	{
		ans=max(ans,sum);
		return;
	}
	dfs(x+1,y,sum+a[x+1][y]);
	dfs(x+1,y+1,sum+a[x+1][y+1]);
}

int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin >> a[i][j];
	dfs(1,1,a[1][1]);
	cout << ans;
}

60分，已经剪去了很多不必要的搜索分枝。但依然超时，f[x][y]（从1，1到x，y路径和的最大值）还是有可能被多次计算，还是搜索尝试了所有的情况才确定下最大值的，只是说部分情况被return没有搜索下去，很多状态还是被重复计算了。如果能一次性就确认最大值该多好！以后用到该状态，就可以直接返回了，不用递归下去了。我们将dfs改为返回int值的，表示从（x，y）到最后1层的最大值。之所以这样表示，是及时返回已经求过的f值。

#include <bits/stdc++.h>
using namespace std;
int a[2005][2005],ans,n,f[2005][2005];

int dfs(int x,int y)
{
	if(f[x][y]!=0) return f[x][y];
	if(x==n)
	{
		return f[x][y]=a[x][y];
	}
	int ans1=dfs(x+1,y);
	int ans2=dfs(x+1,y+1);
	return f[x][y]=max(ans1,ans2)+a[x][y];
}

int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin >> a[i][j];
	cout << dfs(1,1);
}

这样，每个（x，y）只需要求1次，一旦有值了，以后就不再计算了，直接返回值即可，状态一共有n(n+1)/2，复杂度自然是O(n2)。

很显然，越靠近底层的值越先确定下来，特别是最后一层， 根本不需要求，就是$a[x][y]$，我们可以选择不用递归，而是倒着直接求出f值。

#include <bits/stdc++.h>
using namespace std;
int a[2005][2005],ans,n,f[2005][2005];

int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			cin >> a[i][j];
	for(int i=1;i<=n;i++)
		f[n][i]=a[n][i];
	for(int i=n-1;i>=1;i--)
	{
		for(int j=1;j<=i;j++)
		{
			f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j];
		}
	}
	cout << f[1][1];
}

既然能够逆推，我们也可以轻松顺推出结果。既然要反着来，对f数组的定义就应该改变一下：从（1，1）到（x，y）路径和的最大值。

#include <bits/stdc++.h>
using namespace std;
int a[2005][2005],ans,n,f[2005][2005];

int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)for(int j=1;j<=i;j++)cin >> a[i][j];
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(i==j) f[i][j]=f[i-1][j-1]+a[i][j];//只能从左上角来
			else if(j==1) f[i][j]=f[i-1][j]+a[i][j];//只能从上边来
			else f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		ans=max(ans,f[n][i]); //从第1层到第n层的最大值的路径终点可能在第n层的任何位置
	}
	cout << ans;
}

总结

以上从搜索到剪枝，再到记忆化搜索，再到逆推型DP，最后到顺推型DP，展现了DP求解问题的正确性和高效性，以及高效的原因：每个状态只求一次，以后需要时，直接返回，不需再去求解。也就是f数组保存了重要信息，利用这个信息转移可以递推求解问题。以下从DP的层面分析，再解数字三角形。

从集合角度分析DP

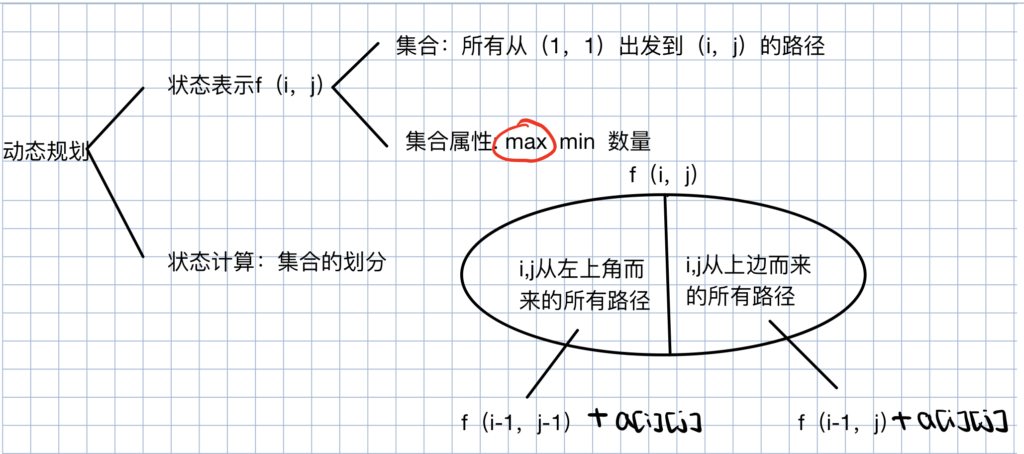
例2 最大连续子序列和

题目描述：

输入n（$n \le 100000$），和n个整数，输出该序列中最大的连续子序列和。

算法一 暴力

#include <bits/stdc++.h>
using namespace std;
int a[100005],n;
long long mx=-1e16;
int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
	{
		cin >> a[i];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=i;j<=n;j++)
		{
			long long sum=0;
			for(int k=i;k<=j;k++)
			{
				sum+=a[k];
			}
			mx=max(mx,sum);
		}
	}
	cout << mx << endl;
}

炸飞！

算法二 前缀和优化暴力

#include <bits/stdc++.h>
using namespace std;
int a[100005],n;
long long s[100005],mx=-1e16;
int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
	{
		cin >> a[i];
		s[i]=s[i-1]+a[i];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=i;j<=n;j++)
		{
			mx=max(mx,s[j]-s[i-1]);
		}
	}
	cout << mx << endl;
}

还是炸！

算法三：DP

f[i] 表示所有以i为结尾的区间的区间和最大值。

集合的划分标准可能不唯一，只要做到不重不漏，且划分的子集是已知的或者已经求解的，则都可以进行正确的动态规划。

#include <bits/stdc++.h>
using namespace std;
int a[100005],n;
long long f[100005],mx=-1e16;
int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
	{
		cin >> a[i];
	}
	for(int i=1;i<=n;i++)
	{
		f[i]=max((long long)a[i],f[i-1]+a[i]);
		mx=max(mx,f[i]);
	}
	cout << mx << endl;
}

例3 最大连续子序列积

输入n(n<=10)和n个整数（包含负数，[-50,50]），输出该序列中最大的连续子序列的积，子序列至少要有一个数。

分析

直接上DP分析图：

如果都是正数的话，那目标区间肯定就是整个区间。但有负数的存在，正负得负，负负得正。问号处就不能填写f[i-1]了，相反，还应该是最小负数。所以仅最大值状态f还不能描述清楚当前的解题需求，显然还需要加1个状态g，表示最小值。为了同步求解这个g，还需要进行同样的动态规划分析。

根据分析写出代码：

#include <bits/stdc++.h>
using namespace std;
long long a[15],f[15],g[15],n,mx;
int main()
{
	cin >> n;
	for(int i=1;i<=n;i++)
		cin >> a[i];
	mx=f[1]=g[1]=a[1];
	for(int i=2;i<=n;i++)
	{
		f[i]=g[i]=a[i];
		if(a[i]>0)
		{
			f[i]=max(f[i],f[i-1]*a[i]);
			g[i]=min(g[i],g[i-1]*a[i]);
		}
		else if(a[i]<0)
		{
			f[i]=max(f[i],g[i-1]*a[i]);
			g[i]=min(g[i],f[i-1]*a[i]);
		}
		mx=max(f[i],mx);
	}
	cout << mx;
}

练习

1. 公路乘车
2. 抢金块
3. 火车票
4. 锁妖塔
5. 美元
6. 架子