基本概念

二叉树由结点的有限集合构成。
这个有限集合要么是空集，要么是一个根节点及两棵互不相交、分别称为这个跟的左子树和右子树的二叉树组成的集合。

二叉树的特点

每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。
左子树和右子树是有顺序的，次序不能随意颠倒。
及时树中某结点只有一颗子树，也要区分它是左子树还是右子树。

二叉树的五种基本形态

1. 空
2. 只有一个根节点
3. 根节点只有左子树
4. 根节点只有右子树
5. 根节点既有左子树，又有右子树

相关概念

• 边（edge）：两个结点（node）的有序对（order pair），称为边
• 结点的度：一个节点含有的子树的个数成为该结点的度
• 叶节点：度为0的结点成为叶节点
• 路径（path）：根节点到某个子节点的”路“
• 路径长度（the length of the paths）：根节点到某个子节点的”路“的长度
• 层数：根是第0层（其他结点的层数等于其父节点的层数加1）
• 深度：层数最大的叶节点的层数

二叉树的性质

1. 在二叉树中，第i层上最多有2ⁱ个节点(i≥0)
2. 深度为k的二叉树最多有2^k+1-1个节点(k≥0)，其中深度的定义(depth)为二叉树层数最大的叶节点的层数
3. 一颗二叉树，若其终端节点数为n₀，度为2的节点数为n₂，则n₀=n₂+1
4. 满二叉树性质：非空满二叉树树叶数目等于其分支节点数+1
5. 满二叉树性质推论：一个非空二叉树的空子树数目等于其节点数+1
6. 有n个节点(n>0)的完全二叉树的高度为log₂(n+1)，深度为log₂(n+1)-1

二叉树的遍历

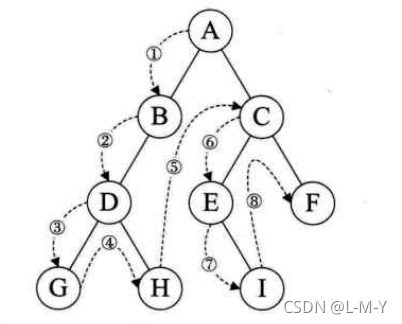
1.前序遍历：先根 再左 再右

规则：若二叉树为空，则操作返回，否则，先访问根节点，然后前序访问左子树，之后前序访问右子树。

代码模版：

#include<bits/stdc++.h>
using namespace std;
struct node{
    int data;//节点
    int left;//左子树
    int right;//右子树
}a[30];
void preorder(int x){//先序遍历
    if(x==0)return;
    cout<<a[x].data;
    preorder(a[x].left);
    preorder(a[x].right);
}
int main()
{ 
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i].data>>a[i].left>>a[i].right;
    preorder(1);
    cout<<endl;
}

2.中序遍历：先左 再根 再右

按中序遍历左子树，访问根节点，然后按中序遍历右子树。

代码模版：

#include<bits/stdc++.h>
using namespace std;
struct node{
    int data;//节点
    int left;//左子树
    int right;//右子树
}a[30];
void inorder(int x){//中序遍历
    if(x==0)return;
    inorder(a[x].left);
    cout<<a[x].data;
    inorder(a[x].right);
}
int main()
{ 
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i].data>>a[i].left>>a[i].right;
    preorder(1);
    cout<<endl;
    inorder(1);
    cout<<endl;
    postorder(1);
}

3.后序遍历：先左 再右 再根

按后序遍历左子树，按后序遍历右子树，然后访问根节点。

代码模版：

#include<bits/stdc++.h>
using namespace std;
struct node{
    int data;//节点
    int left;//左子树
    int right;//右子树
}a[30];
void postorder(int x){//后序遍历
    if(x==0)return;
    postorder(a[x].left);
    postorder(a[x].right);
    cout<<a[x].data;
}
int main()
{ 
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i].data>>a[i].left>>a[i].right;
    preorder(1);
    cout<<endl;
    inorder(1);
    cout<<endl;
    postorder(1);
}

附件：

参考资料：

1. 二叉树的基本操作(C++实现)-csdn