定义
记忆化搜索是一种通过记录已经遍历过的状态的信息,从而避免对同一状态重复遍历的搜索实现方式。
因为记忆化搜索确保了每个状态只访问一次,它也是一种常见的动态规划实现方式。
引入
举个例子,比如「斐波那契数列」的定义是:f0 = 0, f1 = 1, fn = fn-1 + fn-2。如果我们使用递归算法求解第 n 个斐波那契数,则对应的递推过程如下:
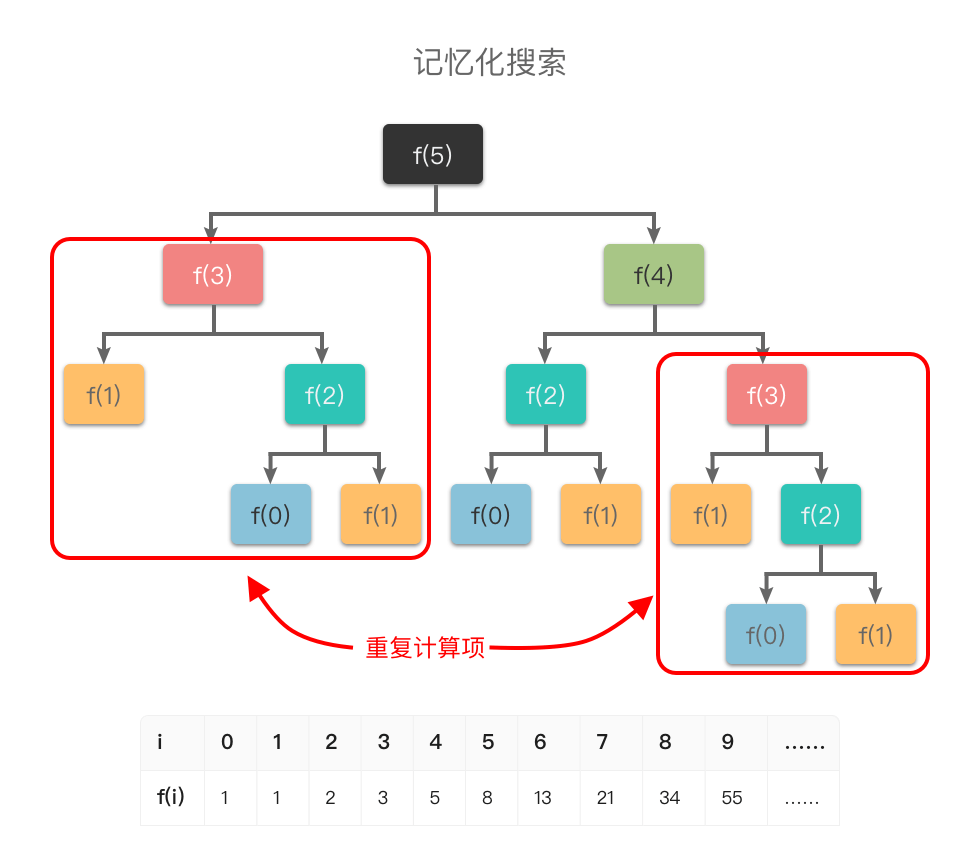
普通的做法是:从图中可以看出:如果使用普通递归算法,想要计算 f5,需要先计算 f3 和 f4 ,而在计算 f4 时还需要计算 f3 。这样 f3 就进行了多次计算,同理 f0 f1 f2 都进行了多次计算,从而导致了重复计算问题。
优化
如果我们每查询完一个状态后将该状态的信息存储下来,再次需要访问这个状态就可以直接使用之前计算得到的信息,从而避免重复计算。这充分利用了动态规划中很多问题具有大量重叠子问题的特点,属于用空间换时间的「记忆化」思想。
f再看本题中,为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来存储已经求解过的 fk 的结果。如上图所示,当递归调用用到 fk 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
使用「记忆化搜索」方法解决斐波那契数列的代码如下:
class Solution {
public:
int fib(int n){
//方法三:记忆化搜索(简单DP)
//找边界
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
//需要定义一个大小为(n+1)的整形数组,并且初始化为0
//之所以是n+1,是因为要使用到n这个下标
vector<int> dp(n+1, 0);
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < n+1; i++)
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};与递推的联系与区别
在求解动态规划的问题时,记忆化搜索与递推的代码,在形式上是高度类似的。这是由于它们使用了相同的状态表示方式和类似的状态转移。也正因为如此,一般来说两种实现的时间复杂度是一样的。
下面给出的是递推实现的代码(为了方便对比,没有添加滚动数组优化),通过对比可以发现二者在形式上的类似性。
int n, t, w[105], v[105], f[105][1005];
int main() {
cin >> n >> t;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= t; j++) {
f[i][j] = f[i - 1][j];
if (j >= w[i])
f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]); // 状态转移方程
}
cout << f[n][t];
return 0;
}在求解动态规划的问题时,记忆化搜索和递推,都确保了同一状态至多只被求解一次。而它们实现这一点的方式则略有不同:递推通过设置明确的访问顺序来避免重复访问,记忆化搜索虽然没有明确规定访问顺序,但通过给已经访问过的状态打标记的方式,也达到了同样的目的。
与递推相比,记忆化搜索因为不用明确规定访问顺序,在实现难度上有时低于递推,且能比较方便地处理边界情况,这是记忆化搜索的一大优势。但与此同时,记忆化搜索难以使用滚动数组等优化,且由于存在递归,运行效率会低于递推。因此应该视题目选择更适合的实现方式。
如何写记忆化搜索
方法一
- 把这道题的 dp 状态和方程写出来
- 根据它们写出 dfs 函数
- 添加记忆化数组
举例:dpi = max{dpj+1} (1≤ j<iaj<ai) 转为:
int dfs(int i) {
if (mem[i] != -1) return mem[i];
int ret = 1;
for (int j = 1; j < i; j++)
if (a[j] < a[i]) ret = max(ret, dfs(j) + 1);
return mem[i] = ret;
}
int main() {
memset(mem, -1, sizeof(mem));
// 读入部分略去
int ret = 0;
for (int j = 1; j <= n; j++) {
ret = max(ret, dfs(j));
}
cout << ret << endl;
}方法二
- 写出这道题的暴搜程序(最好是 dfs)
- 将这个dfs 改成「无需外部变量」的 dfs
- 添加记忆化数组
参考资料(本文由下列资料融合而成)